Programação e matemática não são a mesma coisa
SlidesTable of Contents
- 1. Introdução
- 2. Correspondências interessantes
- 2.1. Philip Wadler
- 2.2. Um pouco de história
- 2.3. Computabilidade
- 2.4. Correspondências interessantes - está tudo interligado!
- 2.5. A matemática é inventada ou descoberta?
- 2.6. A matemática é inventada ou descoberta? - Cont.
- 2.7. Isomorfismo de Curry-Howard
- 2.8. Interpretação algébrica para tipos
- 2.9. Exponenciação como tipos de funções I
- 2.10. Sistemas de tipos
- 2.11. Tipos dependentes
- 2.12. Funções parciais
- 3. Diferenças importantes
1. Introdução
1.1. Essa aula não é sobre
Essa aula não é sobre:
- “Precisa saber matemática pra programar?”
- “Quem tem base matemática programa melhor?”
… que muitas vezes são derivados de “precisa ter faculdade pra trabalhar com programação?”
Vocês estão cursando Ciência da Computação, então independente disso tudo, vão sim aprender uma base lógica/matemática.
1.2. Essa aula é sobre
Como matemática e programação se relacionam, e a importância de entender as diferenças.
- Métodos Formais são sobre matemática ou sobre programação?
Vamos trabalhar com ambos no mesmo ambiente, e o domínio sobre quando usar uma perspectiva ou outra é a principal habilidade para se escrever uma boa especificação formal.
No geral, nós, programadores, tendemos à perspectiva da programação, e precisamos nos esforçar para descrever algumas coisas na perspectiva matemática.
Para isso, primeiro precisamos entender as semelhanças e diferenças
1.3. Ainda sobre essa aula
Se você gostar muito do conteúdo dessa aula:
- Maravilha, considere fazer TCC/pesquisa sobre um dos assuntos!
- Sinta-se motivado para a disciplina
Se você não gostar da aula e ela só te assustar:
- Calma, a disciplina não vai ser nesse nível de loucura
- Começamos tudo do básico na próxima aula, e a maioria do conteúdo dessa aula nem será visto na disciplina
Pensem nisso como uma apresentação de feira de profissões (para a profissão métodos formais e adjacentes).
2. Correspondências interessantes
2.1. Philip Wadler
A primeira parte dessa aula é baseada na palestra/artigo do Philip Wadler (WADLER, 2015)

2.2. Um pouco de história
Em 1928, Hilbert propõe um desafio intitulado entscheidungsproblem (problema de decisão).
- Ele acredita que existe um possível algoritmo que diz se uma declaração pode ou não ser provada pelas regras de uma lógica.
- Isso é equivalente a afirmar que a lógica é completa: tudo o que é provado é verdadeiro, e tudo o que e verdadeiro é provável.
Gödel prova a incompletude da lógica em 1931 (teorema da incompletude de Gödel). Ele mostra como representar o seguinte teorema em qualquer lógica capaz de representar aritmética:
“Esta declaração não é provável”
- Se for verdade, não é provável
- Se for provável, não é verdade
2.3. Computabilidade
O primeiro computador (ENIAC) surgiu somente em 1946. Na época de Hilbert, o conceito de algoritmo é um conjunto de instruções a ser seguido por um humano.
- Não havia uma definição formal do que é computabilidade/algoritmo
Enquanto as pessoas acreditavam que Hilbert estava correto, não havia necessidade de definir computabilidade.
- Quando alguém encontrar a solução para o problema, a solução será um algoritmo.
Para mostrar que o entscheidungsproblem é indecidível, precisamos da definição de computabilidade
- Para que seja possível mostrar que nenhum possível algoritmo pode resolver o problema.
2.4. Correspondências interessantes - está tudo interligado!
Então, as pessoas começam a tentar definir computabilidade. Surpreendentemente, três pessoas independentemente encontram soluções:
- Em maio de 1935, Alonzo Church define o cálculo lambda
- Em julho de 1935, Kurt Gödel (e seu aluno Kleene) define funções recursivas
- Em maio de 1936, Alan Turing define maquinas de Turing
As três são equivalentes!
2.5. A matemática é inventada ou descoberta?
- (WADLER, 2015) Quais partes dessa imagem um alienígena tem mais chances de entender?
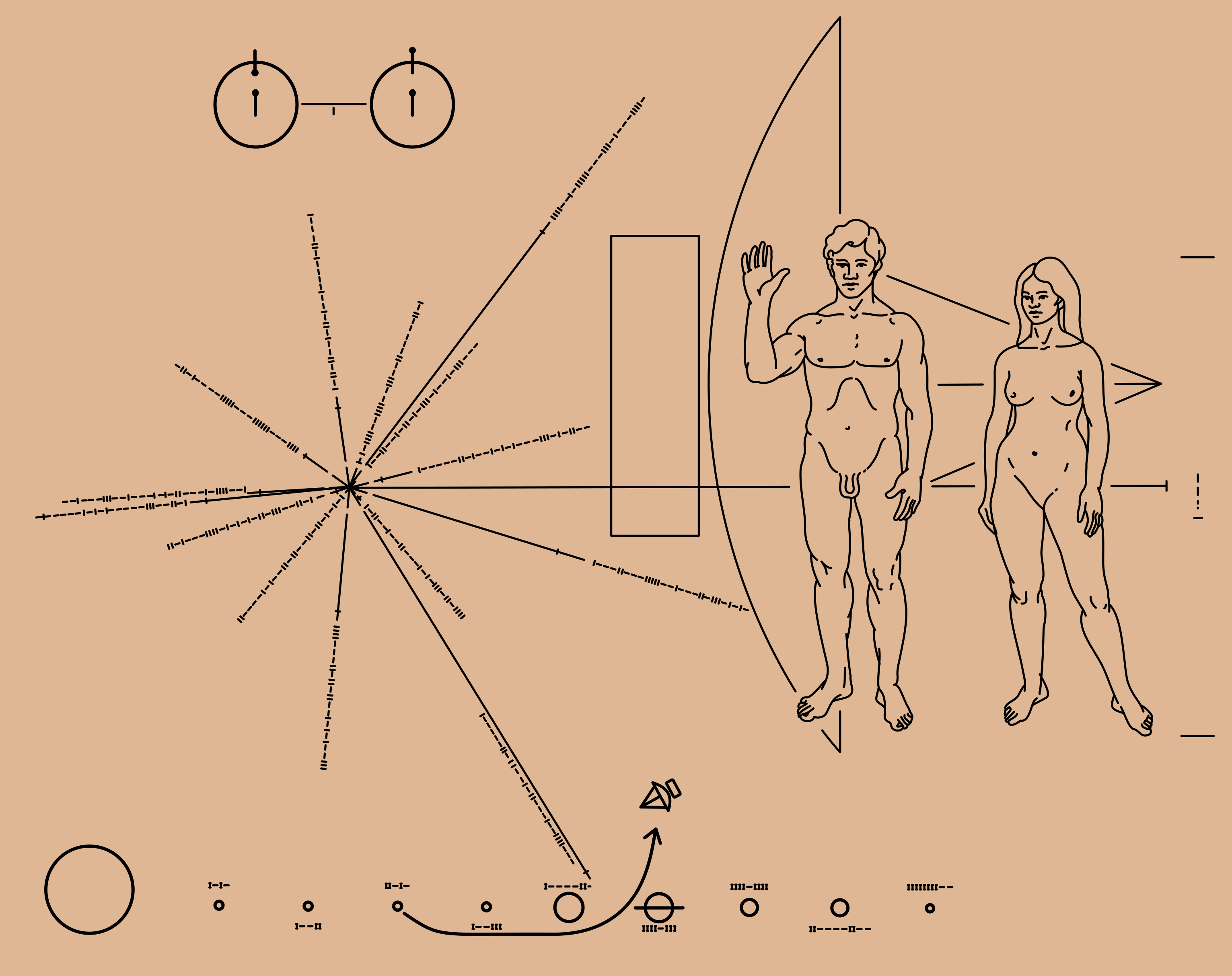
- Quais linguagens de programação eles teriam mais chances de entender?
2.6. A matemática é inventada ou descoberta? - Cont.
Wadler faz uma ótima argumentação de que a matemática é descoberta, o que ressoa muito comigo pessoalmente.
- Se Church, Gödel e Turing tivessem inventado (e não descoberto) essas definições, quais as chances delas acabarem sendo equivalentes?
Vamos ver mais um argumento de Wadler a favor dessa perspectiva: o Isomorfismo de Curry-Howard.
2.7. Isomorfismo de Curry-Howard
- Proposições como tipos
- Provas como programas
- Simplificação de provas como avaliação de programas
| Lógica | Tipos |
|---|---|
| Falso | Void |
| Verdadeiro | () |
| \(a \lor b\) | Either a b |
| \(a \land b\) | (a,b) |
| \(a \implies b\) | a -> b |
Exemplo: implicação e abstração + aplicação
| Lógica | Tipos |
|---|---|
| \({\displaystyle {\frac {}{\Gamma _{1},\alpha ,\Gamma _{2}\vdash \alpha }}{\text{Ax}}} \rule{0pt}{4ex}\) | \({\displaystyle {\frac {}{\Gamma _{1},x:\alpha ,\Gamma _{2}\vdash x:\alpha }}}\) |
| \({\displaystyle {\frac {\Gamma ,\alpha \vdash \beta }{\Gamma \vdash \alpha \rightarrow \beta }}\rightarrow I} \rule{0pt}{8ex}\) | \({\displaystyle {\frac {\Gamma ,x:\alpha \vdash t:\beta }{\Gamma \vdash \lambda x.t:\alpha \rightarrow \beta }}}\) |
| \({\displaystyle {\frac {\Gamma \vdash \alpha \rightarrow \beta \qquad \Gamma \vdash \alpha }{\Gamma \vdash \beta }}\rightarrow E} \rule{0pt}{8ex}\) | \({\displaystyle {\frac {\Gamma \vdash t:\alpha \rightarrow \beta \qquad \Gamma \vdash u:\alpha }{\Gamma \vdash t\;u:\beta }}}\) |
2.8. Interpretação algébrica para tipos
- A teoria das categorias define um nível ainda mais alto de abstração para enxergar algumas coisas. Um dos exemplos mais simples de uma categoria é a categoria dos conjuntos (e das funções entre eles) (DE FRANÇA, 2019).
- As chamadas categorias cartesianas fechadas podem ser relacionadas a nossa álgebra de ensino médio
- A categoria dos tipos é uma delas!
- A categoria dos tipos é uma delas!
| Lógica | Tipos | Álgebra |
|---|---|---|
| Falso | Void |
\(0\) |
| Verdadeiro | () |
\(1\) |
| \(a \lor b\) | Either a b |
\(a + b\) |
| \(a \land b\) | (a,b) |
\(a * b\) |
| \(a \implies b\) | a -> b |
\(b^a\) |
2.9. Exponenciação como tipos de funções I
Vamos escrever tipos função (a -> b) como operações de exponenciação da álgebra:
\(a^0 = 1\) tem assinatura
Void -> a. Apenas uma função tem essa assinatura (em Haskell,absurd)
\(a^1 = a\) tem assinatura
() -> a. O número de funções com esse tipo é o mesmo número de valores do tipoa.
- Por exemplo, pra
asendobool, temosf x = falseef x = true - Qualquer outra versão de
f xpra esse tipo será equivalente a uma dessas duas
- Por exemplo, pra
\(1^a = 1\) tem assinatura
a -> (). Apenas uma função tem essa assinatura (f x = ())
\(a^{b+c}\) tem assinatura
Either b c -> a
- Para definir uma função desse tipo, temos que definir os casos
Leftcom tipob -> aeRightcom tipoc -> a - Ou seja, \(a^{b + c} = a^b * a^c\)
- Para definir uma função desse tipo, temos que definir os casos
\((a^b)^c\) tem assinatura
c -> (b -> a)
- Lembrando de currying, sabemos que isso é equivalente a
(c,b) -> a. - Ou seja, \((a^b)^c = a^{(b*c)}\)
- Lembrando de currying, sabemos que isso é equivalente a
- \((a*b)^c\) tem assinatura
c -> (a, b)
- Equivalente a um par de funções
c -> aec -> b - Ou seja, \((a*b)^c = a^c * b^c\)
- Equivalente a um par de funções
2.10. Sistemas de tipos
- Com tudo o que vimos até aqui, é seguro afirmar que istemas de tipos são uma parte da ciência da computação que tem uma grande intersecção com a matemática
- Sistemas de tipos também são métodos formais: Definimos uma especificação (assinaturas de tipos) e o type checker é nosso sistema de verificação.
- Estudar matemática avançada pode dar base para usos cada vez mais avançados de sistemas de tipos
- Tipos dependentes
- HoTT (Homotopy Type Theory)
- Tipos dependentes
2.11. Tipos dependentes
Tipos dependentes: quando o tipo depende do valor. No exemplo a seguir, usamos o sistema de tipos para provar que a função map não altera o tamanho de um vetor. Isso não é possível sem tipos dependentes.
map : {A B : Set} {n : Nat} -> (A -> B) -> Vec A n -> Vec B n
map f [] = []
map f (x :: xs) = f x :: map f xs
Tipos dependentes são uma parte importante de muitos assistentes de provas (como Coq e Agda). Bem provável que vamos ver mais sobre eles durante os seminários da disciplina.
2.12. Funções parciais
Agora, um caso mais tangível para voltarmos um pouco para a nossa realidade.
Na matemática, funções podem ser totais ou parciais
- Para transformar funções parciais em totais, adicionamos o valor bottom (\(\bot\)) ao co-domínio e mapeamos todos os valores anteriormente indefinidos ao bottom.
- Para transformar funções parciais em totais, adicionamos o valor bottom (\(\bot\)) ao co-domínio e mapeamos todos os valores anteriormente indefinidos ao bottom.
- Na computação, funções parciais precisam retornar o tipo soma. Dependendo da linguagem, pode ser algo como:
f(x: int): int | undefinedint -> Maybe int
3. Diferenças importantes
3.1. Erros vs indefinições
- Na matemática, algumas fórmulas são indefinidas.
- Divisão não está definida para denominador \(0\)
- Exponenciação não está definida para \(0^0\)
- Divisão não está definida para denominador \(0\)
- Na programação, precisamos definir o que acontece nesses cenários
- Normalmente, o que queremos é reportar algum tipo de erro
- Programação envolve humanos. Humanos erram e precisam entender aonde erraram.
- “Opa, você tentou dividir por 0 na linha X coluna Y” - pode salvar alguém de horas de debugging
- “Opa, você tentou dividir por 0 na linha X coluna Y” - pode salvar alguém de horas de debugging
- Normalmente, o que queremos é reportar algum tipo de erro
3.2. Funções vs Maps
Funções matemáticas podem ser programadas através de funções ou Maps (KONNOV, 2024). Pense nos exemplos
- Função de um número para seu dobro.
- Função do nome da pessoa para sua idade.
Na programação, vamos considerar os fatores
- Uso de Memória
- Velocidade de resposta
Numa especificação formal, memória e velocidade não importam da mesma forma
3.3. Implementação vs definição
Imagine a seguinte definição:
- Dada uma função que ordena uma lista de inteiros
O que você pensou sobre essa função?
Bem possível que pensou em um ou mais algoritmos de ordenação (i.e. bubble sort, selection sort, quick sort)
Na matemática, não importa como a ordenação é feita. A função em questão poderia ser descrita mais precisamente por:
- Seja \(f: \overline{\mathbb{Z}} \rightarrow \overline{\mathbb{Z}}\) tal que \(f(x)_i \leq f(x)_{i+1}\) para todo \(i \in [0, |x|-1)\)
Numa especificação formal, se não há relevância no algoritmo de ordenação (contanto que ele, de fato, ordene), podemos economizar recursos na verificação ao especificar somente a propriedade de ordenação.
3.4. Em resumo
- Matemática e programação estão muito interligados
- Contudo, há diferenças nos níveis de abstração entre o que costumamos descrever em definições matemáticas e em programas.
- Em programas, nos importamos com memória e velocidade, o que normalmente não é representado na matemática.
- Em programas, precisamos detalhar como cada função é implementada, enquanto na matemática podemos somente definir funções pelas suas propriedades.
- Inclusive, precisamos detalhar o que acontece em casos indefinidos pela matemática, como divisão por 0.
- Inclusive, precisamos detalhar o que acontece em casos indefinidos pela matemática, como divisão por 0.
- Em programas, nos importamos com memória e velocidade, o que normalmente não é representado na matemática.