1.1 Propriedades

Propriedades podem ser propriedades de segurança (safety properties), vivacidade (liveness properties) ou uma combinação das duas.

1.2 Segurança

"Algo ruim não acontece"

Descreve algo específico. Basta esse algo acontecer uma única vez para que a propriedade seja violada.

Exemplos:

• "O saque não deve ser autorizado, a menos que uma senha correta tenha sido digitada"
  
• "Dois processos não devem estar na seção crítica ao mesmo tempo"
  
• "Ao receber um saque, eu fico com mais dinheiro do que eu tinha antes"

1.3 Segurança - Invariantes

1. Definição

   Invariantes são um tipo de propriedade de segurança.

   Uma invariante é uma propriedade sobre um estado, não sobre uma execução. Uma invariante não consegue "ver além" de um único estado.

   Uma execução satisfaz uma invariante sse cada estado da execução satisfaz a invariante.
   Uma estrutura de Kripke satisfaz uma invariante sse cada estado alcançável satisfaz a invariante.

2. Representação

   

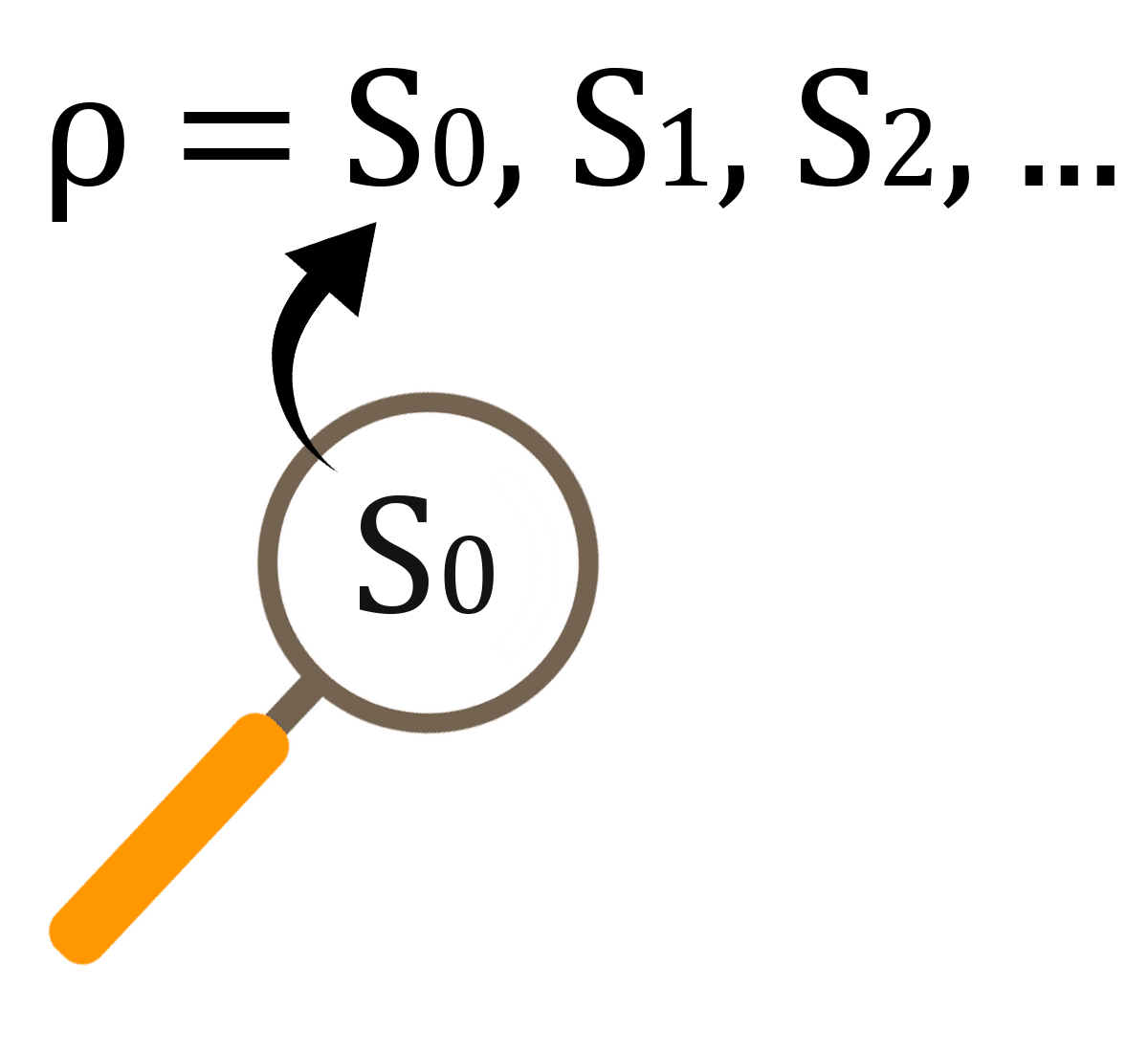
1.4 Vivacidade

"Algo bom eventualmente acontece"

\(\Diamond F\)

Exemplos:

• "Se um processo pediu pra entrar na seção crítica, ele eventualmente deve conseguir"
  
• "Cada sinaleiro deve sempre eventualmente ficar verde"

Lembrando que em Quint e TLA+ usamos LTL, não CTL. Portanto, as fórmulas devem ser verdadeiras em todas as execuções.

1.5 Vivacidade - propriedade de persistência

"Eventualmente, algo é satisfeito pra sempre"

\(\Diamond\square F\)

Exemplos:

• Ao entrar na faculdade, eventualmente vou ter um diploma
  
• Eventualmente estaremos mortos
  
• Eventualmente teremos cabelos brancos ou calvice
  
• Eventualmente as partes chegam em consenso

1.6 Demonstrando vivacidade com runs em Quint

Uma forma alternativa de mostrar que "coisas boas acontecem" em Quint é através de runs.

• Uma run pode definir uma ou mais execuções onde algo acontece.
  • Não serve para mostrar que algo acontece em todas as execuções, como a propriedade em si
    
• Útil quando queremos demonstrar que algo acontece em algumas execuções, mas não necessariamente todas.

Por exemplo, se queremos saber se é possível, em algum cenário, chegar em consenso. Podemos definir uma run semelhante a:

1. Estado inicial
   
2. Processo 1 propõe "A"
   
3. Processo 2 propõe "A"
   
4. Trocas de mensagens seguindo protocolo de consenso
   
5. Processos 1 e 2 decidem "A"

1.7 Fairness (razoabilidade)

Propriedades de razoabilidade (Fairness properties)

• Razoabilidade incondicional (Unconditional fairness): "Algo acontece com frequência infinita"

  • Razoabilidade forte (Strong fairness): "Algo acontece com frequência infinita se é habilitado com frequência infinita"
    
  • Razoabilidade fraca (Weak fairness): "Algo acontece com frequência infinita se é continuamente habilitado a partir de um certo momento"

Usamos essas propriedades como pré-condições para descartar execuções não realistas.

• \(WF(...) \rightarrow F\)
  
• \(SF(...) \rightarrow F\)

1.8 Fairness - definições precisas

Primeiramente, precisamos definir passos balbuciantes (stuttering steps): são aqueles em que o valor de uma variável ou de um conjunto de váriáveis não se altera.

• Por exemplo, x' = x é um passo balbuciante para a variável x.

Operador enabled (ativado):

• \(A\) (ou enabled(A) em Quint) para uma ação \(A\) é verdadeiro em um estado \(s\) sse é possível fazer um passo \(A\) a partir de \(s\).
  
• Ou seja, se existe um estado \(t\) tal que o passo \(s \rightarrow t\) satisfaz \(A\).

Seguem definições precisas copiadas do meu TCC (traduzidas do livro do Lamport (LAMPORT, 2002)).

• Infelizmente não tem como simplificar essas definições, mas tenham em mente que elas estão aqui por questões de completude.

1.9 Weak fairness - definição precisa

A razoabilidade fraca para uma fórmula de estado \(f\) e uma ação \(A\) é escrita como \(WF_f (A)\).

• É satisfeita por um comportamento sse \(A \land (f' \neq f)\) é infinitamente não ativável () ou infinitos passos \(A \land (f' \neq f)\) ocorrem.
  
• Garante que \(A\) não possa permanecer continuamente ativável para sempre sem que um passo \(A\) ocorra. Essa condição pode ser escrita de forma equivalente como
  • \(\square (\ENABLED A \implies \Diamond\langle A\rangle_f)\)

A conjunção com \((f' \neq f)\), expressada com a notação \(\langle A\rangle_f\), se deve ao fato de não ser desejável exigir que passos balbuciantes eventualmente ocorram.

• \(A \land (f' \neq f)\) pode ser lido como "todos os passos não balbuciantes que satisfazem \(A\)".

1.10 Strong fairness - definição precisa

A razoabilidade fraca recebe a denominação "fraca" porque exige que uma ação permaneça continuamente ativável para garantir a ocorrência de um passo que a satisfaça.

• Se um comportamento repetidamente tornar a ação ativável e em seguida não ativável, a razoabilidade fraca não garante nada sobre a ocorrência da ação neste comportamento.
  
• Para tal, é necessário garantir a propriedade de razoabilidade forte (strong fairness).

A razoabilidade forte para uma fórmula de estado \(f\) e uma ação \(A\) é escrita como \(SF_f (A)\).

• É satisfeita por um comportamento sse \(A \land (f' \neq f)\) ocorre finitas vezes ou infinitos passos \(A \land (f' \neq f)\) ocorrem.
  
• Garante que \(A\) não possa ser repetidamente ativável para sempre sem que um passo \(A\) ocorra.

1.11 Fairness na prática

Usamos fairness para "excluir" cenários que não são realistas mas podem causar loops no modelo.

• "loops irrealistas não ocorrem" implica em "coisa boa eventualmente acontece"

2.1 Propriedades temporais em Quint e TLA+

O Apalache atualmente tem algumas limitações para fórmulas temporais, então vamos usar o TLC.

O Quint ainda não está completamente integrado ao TLC. Para usar Quint com TLC, temos um script check_with_tlc.sh no repositório do Quint.

Vamos usar somente TLA+ nos testes da aula de hoje. De qualquer forma, veremos as sintaxes nas duas linguagens.

2.2 Sintaxe

\(\square F\), Sempre, Always:

• []F (TLA+)
  
• always(F) (Quint)

\(\Diamond F\), Eventualmente, Finalmente:

• <>F (TLA+)
  
• eventually(F) (Quint)

Razoabilidade forte e fraca (weak fairness e strong fairness) de uma ação A exigindo mudanças nas variáveis vars

• WF_<vars>(A) e SF_<vars>(A) (TLA+)
  
• weakFair(A, vars) e strongFair(A, vars) (Quint*)

2.3 Operador leads to (leva a)

TLA+ também define o operador temporal ~> lido com leads to.

• F ~> G determina que, sempre que F é verdade, G deve ser verdade eventualmente
  
• Equivalente a \(\square (F \rightarrow \Diamond G)\)

Não existe leads to em Quint, mas podemos definir a versão equivalente:

• always(F implies eventually(Q))

PS: Não confundir com until ou release da lógica temporal.

2.4 Verificando propriedades temporais

Em Quint (instável):
quint verify --temporal minha_propriedade arquivo.qnt

• PS: as formulas em Quint devem ser escritas em definições do modo temporal
  • i.e. temporal minha_propriedade = eventually(true)

Em TLA+ (com TLC):

• No arquivo .cfg, adicionar:

  PROPERTY
  MinhaPropriedade

• Depois, só rodar o model checker normalmente.

2.5 Especificação dos semáforos

Vamos verificar duas propriedades temporais para a especificação dos semáforos.

EventualmenteAbre == WF_<<cores>>(Next) =>
  \A s \in SEMAFOROS : <>(cores[s] = "verde")

SeAbriuVaiFechar == WF_<<cores>>(Next) =>
  \A s \in SEMAFOROS : (cores[s] = "verde" ~> cores[s] = "vermelho")

2.6 Especificação da chaleira

2.7 Referências